Simple 40106 oscillator with diode‑based CV input 【引用元の翻訳】
概要
本件は Simple 40106 oscillator with diode?based CV input の翻訳である。
CD40106シュミットトリガを使用したオシレーター回路について詳しく説明する。以下がその概要である。
-
回路の基本構造: CD40106を使用したシンプルなオシレーター回路で、ダイオードを利用したCV（コントロール電圧）入力を持っている。これにより、外部の電圧源によってオシレーターの周波数を制御することが可能である。
-
部品リスト: 必要な電子部品のリストが記載されており、具体的な値や型番も示されている。これにより、実際に回路を組み立てる際に必要な部品を簡単に揃えることができる。
-
回路図: 詳細な回路図が含まれており、各部品の接続方法がわかりやすく示されている。これを参考にすることで、正確に回路を組み立てることができる。
-
動作説明: オシレーターの動作原理や、ダイオードを使ったCV入力の仕組みについて詳しく説明されている。これにより、回路の働きや調整方法が理解しやすくなっている。
-
応用例: 音楽制作やエレクトロニクスの学習に役立つ応用例が紹介されている。例えば、シンセサイザーの一部として使用する方法などが示されている。
本文
1. Circuit Overview
1.1 The 40106 Hex Inverting Schmitt Trigger
この小さな発振器モジュールは、MFOS Weird Noise Generator[1]とdlbエレクトロニクスウェブサイトの回路図[2]の組み合わせに基づいている。これらの方形波発生器はどちらも40106 Hex Inverting シュミットトリガーチップを基盤としている。シュミットトリガーは特別な種類のコンパレータである。コンパレータは入力を参照電圧と比較し、入力が参照電圧より高いか低いかによって高いか低い電圧を出力する。シュミットトリガーと通常のコンパレータの違いは、シュミットトリガーは参照電圧を移動させることである。これは最初は少し理解しづらいかもしれないが、（fig 1.1a）で非反転シュミットトリガーとコンパレータを比較してみるとよい。
1.2 40106で音を作る
シュミットトリガーを発振させるためには、抵抗器とコンデンサを追加するだけである（fig 1.2a）。
どの抵抗器とコンデンサでも良いが、最初は100nFのコンデンサと100kΩの抵抗を試してみるとよい。出力とアンプの間にもう一つのコンデンサを置き、その甘美な方形波音を聞いてみると良い。ただし、音量は低く保つこと。9Vの電池を使用している場合、その方形波はピークからピークまで9Vフルに達する。最初は魔法や謎のように感じるかもしれないが、実はかなり単純であり、シュミットトリガーの入力での電圧をコンデンサが変化させ、それが音として聞こえるほどに高速で切り替わることに依存している。コンデンサに電流が供給されると、それを電荷として蓄える。そして、充電されるほど、その二つの端子間の電圧差が大きくなる。コンデンサは充電するだけでなく、機会があると放電し、蓄えた電流を吐き出す。 この充電と放電、そしてシュミットトリガーの出力の反転が、魔法を起こす要因である。
回路に電源を入れたときに何が起こるか考えてみる。t=0（すなわち開始時点）では、コンデンサには電荷がないため、その両側の電圧差は0Vである。これにより、コンデンサの一方の側に接続されているシュミットトリガーの入力は0Vを見る。シュミットトリガーは反転シュミットトリガーであるため、高出力になる。つまり、シュミットトリガーの出力は5Vまたは9V（またはチップに供給している電圧）にジャンプする。ただし、話を簡単にするためにここからは5Vで進める。さて、我々は巧妙に、抵抗器を介してシュミットトリガーの出力にコンデンサを接続している。これで、抵抗器は一方に5V、他方に0Vを見ており、電流が流れるようにする。この電流はコンデンサに流れ込み、コンデンサはそれに反応して充電し、その両側の電圧降下がますます大きくなる。それは5Vに到達するまで続くが、それを阻むのがシュミットトリガーである。コンデンサに一定量の電荷が蓄えられると、その電圧降下はシュミットトリガーの上限閾値に達する。このとき、シュミットトリガーは0Vにジャンプする。今度は抵抗器が一方に0V、他方に充電されたコンデンサを見ており、再び電流を流し始める。ただし、今度は逆方向に流れている。つまり、電流はコンデンサから出ている電流で、抵抗器を通じて蓄えられた電荷を吐き出している。電荷を吐き出すと、コンデンサの両側の電圧はどんどん低くなり、再び0Vに到達するまで続くが、またもやシュミットトリガーがそれを阻む。コンデンサが十分に放電すると、シュミットトリガーが再び高出力になると予測したならば、お見事である。このオシロスコープのトレースの写真（fig 1.2b）を見れば、この充電と放電の繰り返しを実際に見ることができる。上のトレースは出力、下のトレースはコンデンサとシュミットトリガーの入力の電圧である。
1.3 ピッチの変更
40106を発振器として使用する楽しさと簡便さの一つは、ピッチの変更がいかに簡単かである。必要なのは、抵抗器と直列にポット（可変抵抗器）を接続することだけである（fig 1.3a）。
抵抗を変えるとピッチがどう変わるのか？前述の通り、コンデンサは電流が流れ込むと充電される。抵抗はオームの法則に従い、流れる電流の量を設定することができる。我々はセクション2で周波数を計算する方法について詳述するが、今のところ知っておくべきことは、抵抗が大きいほど電流が少なくなるということだ。電流が少ないほど、コンデンサの充電と放電が遅くなり、それによってピッチが低くなる。逆に、抵抗が小さいほど電流が多くなり、それにより充電と放電が速くなり、ピッチが高くなる。
1.4 ダイオードの追加
ここで、Weird Sound Generatorとdlbエレクトロニクスの影響が発揮される。シュミットトリガーの入力にダイオードを取り付けることで、非常にシンプルな電圧制御を追加した（fig 1.4a）。
これがダイオードのカソード（負の側）をグランドに接続するのと同じである。シリコンダイオードはオンになるために約0.6Vの電圧降下が必要であることを知っておくべきである。オンになった後、ダイオードは事実上任意の量の電流を流すことができる。これは、ダイオードの電圧降下が0.6Vに達した後、アノード（正の側）の電圧がグランドから約0.6V上がることを意味する。入力電圧は0.6Vを超えることはできず、すべての電流はダイオードを通じてグランドに流れ込み、コンデンサには流れない。もし0.6Vを超える電流がコンデンサに流れ込み、それを充電したとしても、ダイオードによって吸い戻される。0.6Vはかなり低い電圧である。シュミットトリガーの上限閾値を思い出してみると、それは電源の2/3程度である。5Vでも閾値は約3.3Vであり、0.6Vよりはるかに高い。これにより、コンデンサはシュミットトリガーの出力を変えるのに十分な高電圧まで充電できず、発振が停止する。
次に、CV入力が5Vの場合を見てみる（fig 1.4c）。
CVが5Vの場合、ダイオードは逆バイアスされる - 電流が流れることはない。これは、アノード側の電圧が5.6V（カソードに必要な0.6Vより高い）に到達する方法がないためである。理由は二つある：回路は5Vまでしか上がらないため、5.6Vは不可能である；たとえ可能であったとしても、シュミットトリガーがフリップし、電圧がそこに到達する前にコンデンサが放電を始めるためである。これにより、CVが5Vのとき、発振器は再び発振することになる。これが最初は少し無意味に思えるかもしれないが、非常に高速なスイッチを作成したことになる。このスイッチは非常に高速で、オーディオレートで発振器をオンオフできる。これにより、オーディオレートCVを投入すると、非常にクールな疑似同期音や、LFOを使用した伝統的なオンオフのトレモロサウンドを作成できる。
1.5 より良いCV制御のためのもう一つのポットの追加
このようなゲーティングと同期音は非常にクールで有用だが、さらに多くのオプションとコントロールがあると良い。ダイオードとCV入力の間にポットを追加することで、それが可能になる。その仕組みは？詳細と数学は次章に譲るが、今はこの一連のオシロスコープトレース（fig 1.5a - d）を見ると非常に助けになるだろう。再び上が出力で、下がコンデンサの電圧とシュミットトリガーへの入力である。抵抗値を上げると、CVが0Vの時のフラットな部分が上昇し、発振を許すほど高くなる。これは、ダイオードがオンになるために電流を供給する必要があるためである。これが行われると、電流はCV量のポットを通じて流れ、ポットの抵抗として使用され、電流の流れがポット全体での電圧降下を引き起こす。ダイオードの約0.6Vの電圧降下はこの電圧降下に加算され、コンデンサが充電できる電圧も上昇する。ここでもう一つの要素が関与しており、それが実際のピッチコントロールを提供する。ダイオードの膝特性（knee）である。
オシロスコープのトレース（fig 1.4d）を見れば、コンデンサの充電が直線ではなく、明らかに曲線になっていることに気付くだろう。これは、ダイオードの導通の小さな領域で、電流がゆっくりと増加するためである。また、充電速度が大きく影響されることにも気付くかもしれない。その結果、発振器のピッチを変更すると、デューティサイクルも変更される。出力はもはや50/50の波形に近くなくなる。代わりに、ピッチの変更により出力が高い状態の時間が長くなり、波形の低い部分は以前とほぼ同じ長さになる。
2. Analysis
2.1 発振器の周波数の計算
残念ながら、40106を発振器として使用することには一つの欠点がある：すべてのチップに対して正確な周波数を計算することができないことである。これは、各ICごとに上限閾値と下限閾値が異なる小さな違いが原因である。幸いなことに、これはそれほど大きな問題ではない。特に次の偉大なポリシンセを構築しようとしているわけではないので、正確さはそれほど重要ではない。National Semiconductorのデータシートを見ると、どれだけの変動があるかを知ることができる（fig 2.1a）。
National Semiconductorのデータシートには、使用している発振器の例も含まれており、以下の周波数の式が提供されている。
$$ \begin{aligned} f \approx \frac{1}{RC \cdot \ln \left( \cfrac{V_{T+} \cdot (V_{DD} - V_{T-})}{V_{T-} \cdot (V_{DD} - V_{T+})} \right)} \end{aligned} $$今はただ恐ろしい数学の混乱のように見えるかもしれないが、恐れることはない。一歩一歩進んでいく。
2.1.1 RC時定数
周波数を計算する最初のステップは、コンデンサがどれだけ速く充電および放電するかを見極めることである。前述の通り、抵抗が大きいほど遅く、小さいほど速くなる。幸運なことに、ある賢いエンジニアがこの非常に重要でありがたいことにシンプルな方程式を考案した： $$\tau = RC$$
ギリシャ文字の $\tau$（「タウ」）は、コンデンサが初期値と目標値の差の約63.2％に達する時間、または約36.8％に放電する時間を表す。約63.2％と約36.8％は一見奇妙な数字に思えるかもしれないが、実際には数学定数の $e$ に由来する。ここからは $\tau$ を使用せず、単に $RC$ を使用する。これは、秒単位の時間を表すときに混乱を避けるためである。
簡単な抵抗器がコンデンサを充電する回路（fig 2.1.1a）を再び考えてみる。
スイッチをオンにすると（t=0）、コンデンサは完全に空であり、両端とも0Vである。つまり、抵抗器には5Vがかかる。オームの法則により、抵抗器を流れる電流を簡単に計算できる。$I = V/R$ なので、$5V / 5kΩ = 0.1mA$ である。
しかるに、コンデンサに流れる電流のたびに、コンデンサは充電される。充電されると、その端子間の電圧降下が増加する。これにより、抵抗器の電圧降下が縮小し、電流が減少し、結果的にコンデンサの充電速度が遅くなる。これは、コンデンサが5Vに達するまで続き、それ以降は電流が流れない。幸運なことに、この現象は前述の定数$e$のおかげで簡単にグラフ化できる。
$V(t)$ は、$t$秒後のある時点での電圧を表す。1秒後の電圧を求めるには、右辺の$t$を1に置き換えれば良い。2秒後ならば2に置き換える。ここで、$V_0$ はコンデンサにかかる電圧とその目標の差を意味する。我々の単純化した回路では、充電時には0Vから5Vまで充電するため、5Vを意味する。放電時には、5Vから0Vまで下がるため、再び5Vを意味する。
なぜ約63.2％と36.8％なのか？これは、$t = RC$ の時、$-t/RC = -RC/RC$ となり、$-t/RC = -1$ だからである。$e^{-1}$ は約0.368である。
2.1.2 シュミットトリガー出力の変動を考慮する
前述のように、コンデンサが充電されるときの目標は5Vである。しかし、コンデンサがその目標に到達する前に、シュミットトリガーが低出力に切り替わる。類似して、出力が切り替わった後、コンデンサは0Vに向かって放電を開始するが、これも完全には達成されない。これは、回路の充電および放電サイクルの開始点に影響を与えるため、$V_0$を調整して補正する必要がある。これが、使用するチップを正確に測定せずに正確さを維持するための製造上の不一致の部分である。代わりに、汎用的な式を考案することになる。まず、サイクルの放電部分がどのように影響されるかを見てみる。
2.1.3 コンデンサが下限閾値に放電する時間の計算
正確な答えを得るためには、コンデンサの放電式を少し調整する必要がある。$V_0$を何に置き換えるかを見極める必要がある。$V_0$は常に初期電圧と目標電圧の差である。この例では、解は簡単である。それはシュミットトリガーの上限閾値$V_{T+}$である。これは、シュミットトリガーの入力がこの電圧に達すると出力が低くなり、放電が始まるためである。コンデンサに関して言えば、目標はグランドまで放電することなので、初期値と目標の差は次のようになる： $$V_0 = V_{T+} - 0 = V_{T+}$$
次の式でそれがどのように見えるかを示すことができる： $$V(t) = V_{T+} \cdot e^{-t/RC}$$
入力の電圧が下限閾値に達するまでにかかる時間を求めるためには、$V(t) = V_{T-}$ となる$t$を見つける必要がある。
$$V(t_{discharge}) = V_{T-} = V_{T+} \cdot \left(e^{?t/RC}\right)$$
両辺を$V_{T+}$で割って、 $$\frac{V_{T-}}{V_{T+} } = e^{-t/RC}$$
x = ay のとき, y = loga(x) なので、
$$-\frac{t}{RC} =\ln \ \left(\frac {V_{T ?}}{V_{T +}}\right)$$
両辺に$RC$をかけて、
$$-t =RC \cdot \ln \ \left(\frac {V_{T ?}}{V_{T +}}\right)$$
$\log_a(x/y) = ?\log_a(y/x)$なので、
$$t_{\text{discharge}} = RC \cdot \ln \left( \frac{V_{T+}}{V_{T-}} \right)$$
2.1.4 コンデンサが上限閾値に充電する時間の計算
今回は、コンデンサが$V_{T-}$から電源電圧$V_{DD}$に向かおうとしているため、同じ手順で計算する。ただし、$V_0$を適切に調整する必要がある。 $$V_0 = V_{DD} - V_{T-}$$
CMOSチップを扱う際、通常は正の電源電圧を$V_{DD}$と呼ぶ。また、コンデンサが既に部分的に充電されている事実を考慮するため、結果に$V_{T-}$を加える。 $$V(t) = (V_{DD} - V_{T-})(1 - e^{-t/RC}) + V_{T-}$$
今回は、コンデンサの電圧が上限閾値$V_{T+}$に達する時を知りたいので、$V(t)$を$V_{T+}$に置き換える。再び、左辺に$t$のみが残るように整理する：
$$ V(t_{charge}) = V_{T+} = V_0 \left(1 - e^{-t/RC}\right) + V_{T-} $$ カッコを取って整理すると、 $$V_{T+} = V_0 - V_0 \left(e^{-t/RC}\right) + V_{T-}$$ 両辺から$V_0$と$V_{T-}$を引いて、 $$-V_0 \left(1 - e^{-t/RC}\right) = -V_0 + V_{T+} - V_{T-}$$ 符号を逆にして、 $$V_0 \left(e^{-t/RC}\right) = V_0 - V_{T+} + V_{T-}$$ 両辺を$V_0$で割る。 $$e^{-t/RC} = \frac{V_0 - V_{T+} + V_{T-}}{V_0}$$ $V_0 = VDD ? V_{T-}$なので、 $$e^{-t/RC} = \frac{V_{DD} - V_0 - V_{T+} + V_{T-}}{V_{DD} - V_0}$$ 右辺の分子を整理する。 $$e^{-t/RC} = \frac{V_{DD} - V_{T+}}{V_{DD} - V_{T-}} \qquad (V_{T-} - V_{T-})$$ 対数で表すと、 $$t_{charge} = -RC \ln \left(\frac{V_{DD} - V_{T+}}{V_{DD} - V_{T-}}\right)$$
2.1.5 結果をまとめて周波数を得る
これで、コンデンサが上限閾値から下限閾値に移動し戻るまでの時間の式が得られたので、発振器の周波数を求めるのは簡単である。両方の結果を足して逆数を取るだけである。時間（秒単位）は周波数（Hz単位）の逆数である。 $$f = \frac{1}{t}$$ $$t = \frac{1}{f}$$
この関係と以下の代数学の規則を考えると： $$a\log_b(x) + a\log_b(y) = a\log_b(xy)$$ $$a/b + x/y = \frac{ax}{by}$$
データシートにある式が得られる。
$$f \approx \frac{1}{RC \cdot \ln \left( \cfrac{V_{T+} \cdot (V_{DD} - V_{T-})}{V_{T-} \cdot (V_{DD} - V_{T+})} \right)}$$
2.2 ダイオードが回路に与える影響
残念ながら、この時点に来ると、代数を使ってダイオードが周波数に与える影響を計算することは不可能である。これは、ダイオードの動作を数学的にモデル化することが非常に難しいためである。すべての半導体と同様に、ダイオードは温度の変化によって影響を受ける。また、ダイオードのために作る任意の式は超越的である。これは、$x = \cos(x)$のように、代数的な解がないことを意味する。唯一の解決方法は、反復を通じて解くことであり、それには多くの忍耐力かコンピュータが必要である。幸いにも、正確さにこだわらないので、シンセサイザーを使用する際には耳に頼ることができる。しかし、コンデンサがどれだけ充電されるかの上限をかなりの精度で予測することはできる。これにより、あるCV電圧とCV量ポットの抵抗が発振を停止させるかどうかを見極めることができる。
2.2.1 非常に簡略化されたダイオードモデル
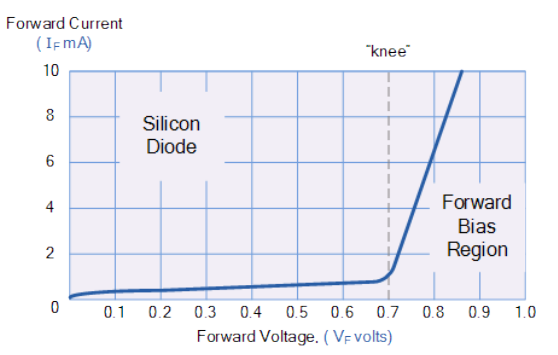
ダイオードを非常に正確にモデル化する方法があるが、適度な精度でダイオードをモデル化するさらに簡単な方法もある[1]。ここでは、さらに簡単なモデルを選択する。この利点は、計算が非常に簡単になることである。したがって、シンプルさの名の下に、ダイオードは電圧降下が0.6Vに達するまで絶対に電流を流さず、その後無限の電流を導通する魔法のデバイスであると仮定する（fig 2.2.1a）[2]。
残念ながら、（fig 2.2.1b）[3]のより正確なダイオードのIVカーブからもわかるように、このモデルは現実とは大きく異なる。
2.2.2 等価回路の作成
ダイオードのモデルができたので、これを使って回路の動作を推定する方法を考える。ダイオードがコンデンサの最大充電電圧をどのように制限するかにしか興味がないため、コンデンサを完全に省いても問題ない（fig 2.2.2a）。
奇妙に思えるかもしれないが、コンデンサが最高電圧まで充電されると、それ以上電流を引かないので、放電されるまで事実上回路から外れる。このため、コンデンサに課される制限を見つけるには、点xの電圧を求めるだけで良い。オームの法則のおかげで、基本的にはR1を流れる電流を求め、その電流を使って電圧降下を計算することになる。
2.2.3 抵抗を通る電流の計算
回路が単なる直流の線形回路であるため、回路内のすべての点で電流は同じである必要がある。2つの抵抗とダイオードが直列に接続されているため、電流はそれらの抵抗の高さに直接関係する。ダイオードがなければ、2つの抵抗を合計し、CVをVDDから引いて、すべてをオームの法則に当てはめるだけで簡単である。しかし、ダイオードがあると、余分な0.6Vを考慮に入れる必要があるため、少し複雑になる。幸いなことに、これは非常に簡単である。回路全体が0.6V少ないと見なせば良い。ダイオードの電流消費については気にする必要はない。少なくとも非常に簡略化されたモデルでは無限である。
$$ I = \frac{V_{DD} - V_{CV} - 0.6V}{R_1 + R_2} $$
これで流れる電流がわかったので、次にすることはR1にかかる電圧降下を計算し、それをVDDから引くことである。 $$V_{limit} \approx V_{DD} - \frac{R1 \cdot (V_{DD} - V_{CV} - 0.6V)}{R1 + R2}$$
再度述べておくが、これは正確ではない。しかし、約±10mVの精度であり、これはかなり良い。ここから知るべきことは以下の通りである： $$V_{limit} > V_{T+}$$
2.2.4 ダイオードCV方式の欠点
最後に一つ、大きな欠点を挙げておく必要がある。この方法でCVにダイオードを使用すると、結果が$R_1$、すなわちピッチポットに非常に依存することがわかるだろう。これにより、低いピッチでは、CVが周波数を変調したり、発振を許可したりするのが難しくなる。ただし、部品の数が非常に少なく、この方法で単純なCVを実装するのが非常に簡単であることを考えると、それでも非常に価値があると考える。
3.改良
3.1 ピッチポットの「感触」を改善
ピッチポットはCテーパー（逆ログ）ポテンショメータに置き換えるか、ポットの使用する二つのラグに4-5MΩの抵抗を並列に接続することで改善できる。これにより、周波数ポットの回転全体にわたってより一貫した感触が得られ、オクターブごとの応答に近づく。
3.2 CVトリムポット
トリムポットをダイオードおよびCV量ポットと直列に追加することで、発振が開始する位置を調整する「セット＆忘れ」変更を簡単に行うことができる。また、特定の周波数以上でのゲーティングを防ぐこともできる。