平滑コンデンサ 容量 目安

CRω ≧ 30 の導入

交流を直流にするために、まず「整流」を行う。

半波整流回路、全波整流回路、ブリッジ整流回路など、さまざまな整流回路があるが、「整流」された後の電圧は以下の点線の山ような波形が出てくる。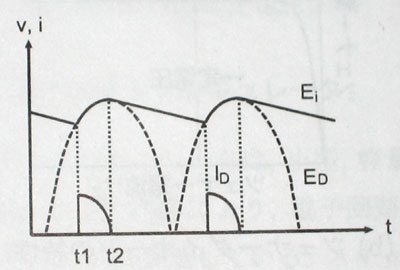

（ブリッジ整流後の波形、スイッチングACアダプターなどはほとんどこんな感じ）

「整流」しただけでは、このように山が連なっただけのデコボコだ。
このままでは直流と呼ぶには程遠い。

このデコボコを解消するために「平滑」を行う。

「平滑」することで、実線のような、デコボコに比べればマシな波形にできる。
平滑回路にも、コンデンサ入力型、チョーク入力型、π型などさまざまなものがあるが、一般に簡単でよく使われる以下の図のようなコンデンサ入力型について説明する。

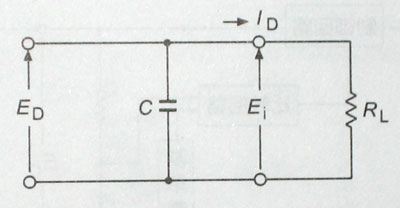
この回路で、Cが電源平滑コンデンサ、R_Lがスピーカーなどの負荷インピーダンスだ。
Cに電荷が貯まることにより、負荷の電圧E_iは図の実線のような波形になるのだ。

この原理について説明する。
入力電圧E_Dが山が連なったような形の波である。
このE_Dの上昇によりCに電荷が貯まっているのがt1〜t2の期間だ。
コンデンサに電荷が貯まる速度は一般に速く、ほぼ入力電圧E_Dに追随する。
これに対し、右肩下がりに直線的に下がっているところが、コンデンサが放電している期間だ。
放電時間は、コンデンサ容量と負荷抵抗の積（C・R_L）で表される時定数により決定される。
コンデンサ容量Cが大きいと時定数が大きくなる、つまり放電するのに時間がかかるため、 入力電圧E_Dの変化に追随しなくなる。
その結果、 入力電圧E_Dの波形に比べなめらかになった図の実線のような波形になる。

ここで、リップル含有率を導入する。因みにリップル（ripple）とはさざなみという意味だ。
リップル含有率とは、直流電圧の大きさに対する、電圧の揺れを表したもの。
リップル含有率をγと表すとすると、

と定義されている。
ここで、
V：直流電圧の大きさ（平均）
V_a：電圧の揺れ（デコボコの大きさ）
である。

リップル含有率が小さいほど、より直流に近い電源であると言える。

リップル含有率がα×100[％]以下になるように平滑コンデンサの容量を決定する式を求める。
商用電源の周波数fは関東では50Hz、関西では60Hzだ。
よって、整流した２山分の時間（周期）は

より、関東ではT=0.020sec、関西ではT=0.0167secである。

時定数（C・R_L）が１山分の時間（T/2）に比べて十分に大きければ、ゆっくり放電している間に、次の入力電圧E_iが上昇してきて追いつくことになるので、デコボコは小さくなる。

コンデンサの放電曲線は本来、指数関数的に過渡応答を示すが、T/2が時定数に比べて小さい範囲を考えるので、直線近似する。
また、放電曲線とsinカーブがぶつかる点は3T/8であると近似することにより、次式が得られる。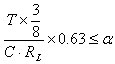

Cについて解くと

となる。ここで、定数の0.236 は3/8 x 0.63 = 0.236 のことである。

リップル含有率α=0.05のとき、上記の式を変形すると、

CRω ≧ 2π x 0.236 / 0.05 = 29.6 になる。α = 0.03 では、CRω ≧ 49.4　である。

したがって、CRω ≧ 30～50 （リップル含有率α 0.03～0.05）が平滑コンデンサの容量めやすとされている。

具体例