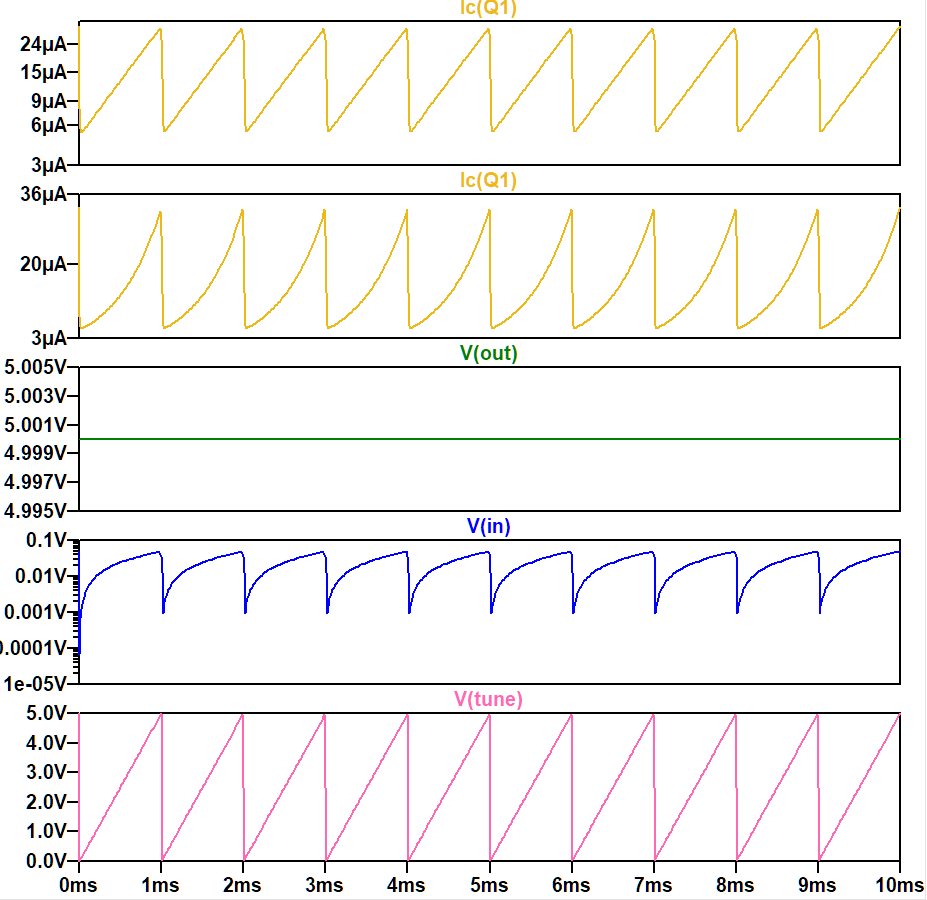
アンチログ回路のいろは

2023/ 11/ 02    2025/ 06/ 28
**概要**

概要

以下のブログを読みながら、自分で理解できるようにまとめ（パクリ）ました。

アナログシンセの VCO ブロック (3) -- アンチログ回路(2) - シンセ・アンプラグド

アナログシンセの VCO ブロック (3) -- アンチログ回路(2) - シンセ・アンプラグド

実際のアンチログ回路としては、ふたつのトランジスタを差動対の形で組み合わせ、OP アンプで定電流回路を構成したものが使われます。 まず、トランジスタ Q1, Q2 のエミッタは接続されているので、 より、 が成り立ちます。 これで、前述の の式の指数関数の引数に表れる の差と を結びつけることができました。

  ファビコンpcm1723.hateblo.jp

本文

アンチログ回路の基本原理

BJT
トランジスタの立ち上がり部分では、ベース・エミッタ間電圧 Vbe とコレクタ電流 Ic の関係は非線形で、以下の式で近似できます。

$$I_C = a \cdot I_S \cdot ( \exp (\cfrac{q\cdot V_{BE} }{l \cdot k \cdot T} ) - 1) \tag1 $$

ここで、

  • q : 電子の電荷 1.6e-19 [C]
  • $k$ : ボルツマン定数 1.38e-23 [J/K]
  • $T$ : 絶対温度 [K]
  • $l$ : Ic に依存する定数。通常は1と仮定する。
  • $V_{BE}$ : ベース・エミッタ間電圧 [V]
  • $I_S$ : 逆方向エミッタ飽和電流（逆方向漏れ電流） [A]
  • a : ベース接地電流増幅率。約 1。
  • $I_C$ : コレクタ電流 [A]

この式で、$T = 300K (27℃)$、$l = 1$とすると、$kT/q$ は約 26mV となり、上記の式は以下のように近似できます。

$$I_C = a \cdot I_S \cdot \exp(\cfrac{q \cdot V_{BE}}{ l \cdot k \cdot T }) \tag2 $$

この式で、指数関数の引数に絶対温度 $T$ が含まれており、温度に依存することが分かりますが、実は逆方向飽和電流 $I_S$ にも温度依存性があり、しかも、複雑な変化をします。 トランジスタ一個だけでは、この複雑な温度依存性を避けられないので、特性の一致したトランジスタを２個使って $I_S$ 依存性をキャンセルすることを考えます。
２個のトランジスタを、添え字 1, 2 で区別します。　トランジスタは熱結合されていて、両者は等しい温度 $T$ に保たれているものとします。ここで、２つのトランジスタの比を考えます。

$$ \begin{aligned} \cfrac{I_{C2}}{I_{C1}} &= \cfrac{a \cdot I_S \cdot \exp(\cfrac{q \cdot V_{BE2}}{ l \cdot k \cdot T })}{a \cdot I_S \cdot \exp(\cfrac{q \cdot V_{BE1}}{ l \cdot k \cdot T })} \\ &=\exp \left[ ( V_{BE2}-V_{BE1})\cdot \cfrac{q}{kT}\right] \tag3 \end{aligned} $$

実際のアンチログ回路としては、ふたつのトランジスタを差動対の形で組み合わせ、OP アンプで定電流回路を構成したものが使われます。

まず、トランジスタ Q1, Q2 のエミッタは接続されているので、

$$ \begin{aligned} V_{E1}&=V_{B1}−V_{BE1}\\ &=−V_{BE1}\\ &=V_{E2}\\ V_{E2}&=V_{B2}−V_{BE2}\\ &=V_{in}−V_{BE2} \end{aligned} $$

より、 $$V_{in}=V_{BE2}−V_{BE1} \tag4$$

式(3)と式(4)より、$\cfrac{I_{C2}}{I_{C1}}$ は$V_{in}$ の関数として表せることがわかります。

ここで、オペアンプのイマジナリーショートの関係より、$V_{C1}=0$ になります。このとき、$I_{C1}=\cfrac{V_{ref}}{R_{ref}}$が強制されます。したがって、式(3)より

$$ \begin{aligned} I_{out}&=I_{C2}\\ &= I_{C1}\cdot \exp \left[ ( V_{BE2}-V_{BE1})\cdot \cfrac{q}{kT}\right] \\ &= \cfrac{V_{ref}}{R_{ref}}\cdot \exp \left[ V_{in}\cdot \cfrac{q}{kT}\right] \tag5 \end{aligned} $$

となります。
ここで、OP アンプは $I_{C2}=I_{out}$ 側の電流も負担していることに注意してください。
OP アンプ出力と、トランジスタのエミッタの間の抵抗には、次のふたつの意味があります。

  • OP アンプ側からみると、トランジスタはベース接地増幅回路に見えるので、抵抗によって電圧-電流変換をしている
  • OP アンプのフィードバックループに障害が生じて OP アンプ出力が電源電圧いっぱいに張り付いた場合に電流制限をして、トランジスタを保護する

特記事項

  1. 通常、エミッタ側の電流制限抵抗はコレクタ側の抵抗より小さいので、ベース接地増幅回路としてはゲインを持つことになります。　OP アンプのフィードバックループ内にゲインを持つ回路が挿入されることになるので、OP アンプの−入力端子と出力端子の間に発振防止のコンデンサが接続してあり、高域でのゲインを抑えています。

  2. 使用する出力電流範囲の最大値を $I_{max}$ 、最小値を $I_{min}$ とすると、$I_{ref}=V_{ref}/R_{ref}$ は相乗平均 $I_{ref}=\sqrt{I_{max}\cdot I_{min}}$ に選ぶのが自然です。　こうすると、入力電圧 Vin の振れ幅が正負等しくなります。

  3. トランジスタのコレクタ電流をそのまま出力電流として利用しているので、そのふるまいは、ほぼ定電流特性となります。　アーリー (Early) 効果の影響もありますが、ベースを低いインピーダンスでドライブすれば、あまり問題になりません。　 これは、高コンプライアンス、つまり、出力端子の電位が、GND 付近から電源電圧付近まで変化しても、電流はあまり変化しないという特長になります。

  4. 前のアナログシンセの VCO の構成の記事で言い忘れていたのですが、この特長により、アンチログの出力に OP アンプを介さず、直接にコンデンサを接続する形式の VCO が構成できます。　その電圧スイングも GND 付近から電源電圧付近まで、ほぼフルに利用できます。

  5. 出力端子、つまりコレクタの電位を GND レベルとして利用する場合、ベースに入力電圧 Vin が加えられていますから、入力電圧が正の場合、ベース・コレクタ間は順方向にバイアスされ、トランジスタは飽和領域に入ることになります。 しかし、実際のところ、アナログシンセの場合 MIDI ノートの全範囲 10.7 オクターブに対して入力電圧の変化は ±100 mV 足らずですから、ほんの軽い飽和に過ぎず、ほとんど能動領域と差はありません。

  6. 実際の回路では、Q2 のベースが GND に固定されており、Q1 のベースがアンチログ部の入力となっています。 これは、前段のサミングアンプが反転型加算回路となっているため、プラスの CV 入力に対してマイナス電圧が出力されるからです。　アンチログ回路は VBE の差に対して動作するので、Q2 のベース電位を上げるのと、Q1 のベース電位を下げるのとは同じ効果をもたらします。

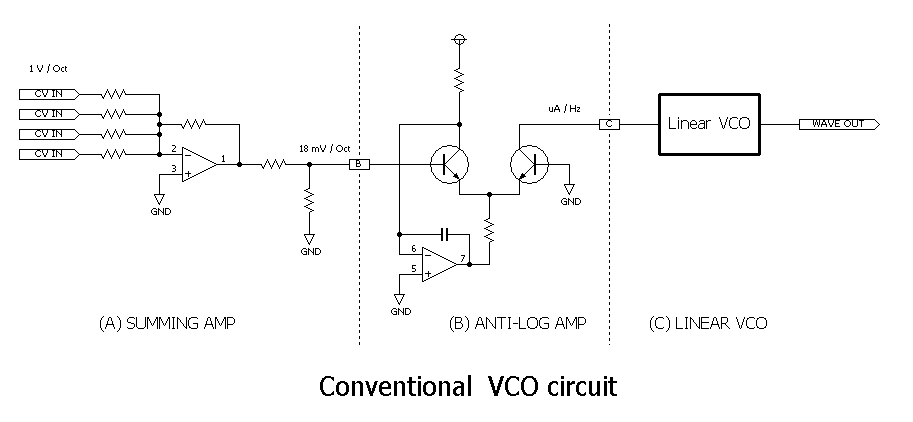
アナログシンセの VCO

x を 1 V/Oct スケールの VCO ブロックへの CV 入力、y をアンチログの出力電流とします。　x はアンチログアンプへの直接の入力ではありません。 x が 1V 増加するたびに y は２倍になる必要がありますから、この関係は、２を底とする指数関数、 $$y=2^x$$ で表されます。 これまでのアンチログ回路の話は自然対数の底 e の指数に関するものでしたから、この式の対数を取ると、$$\ln y=x \cdot \ln 2$$ より、 $$y=2^x=\exp(x\cdot ln(2))\tag6$$

と書き表せます。　

ここで、VCO ブロックへの入力 x が A 倍されてアンチログへ入力される、つまり、$V_{in}=A\cdot x$ と表されると考えます。このとき、式(5)と式(6)の引数が等しくなるようにAを選ぶものとします。すなわち、

$$ \begin{aligned} x\cdot \ln(2)&=A \cdot x\cdot \cfrac{q}{kT} \\ A &=\ln(2) \cdot \cfrac{q}{kT} \end{aligned} $$ となって、スケーリング係数 A が求められます。 $\cfrac{kT}{q}$ は電圧のディメンジョンを持ち$V_T$ (thermal voltage) と呼ばれ、常温 ($T=300K$) で約 26 mV です。しかるに、

$$A=\ln(2) \cdot 26[mV] = 18[mV]$$ です。つまり、VCO ブロックへの 1 V/Oct の CV 入力を 18/1000 倍して、アンチログへ入力するとスケールが合うことになります。

CV 入力を $V_{CV}$ として、基本式を書き直すと、 $$I_{out}=I_{ref} \cdot \exp(A \cdot \cfrac{V_{CV}}{V_T})$$

となります。

アナログシンセでの実例

Analog 2.0風（共通エミッター）

Q2 のベースが GND に固定されており、Q1 のベースがアンチログ部の入力となっています。 これは、前段のアンプが反転型加算回路となっているため、プラスの CV 入力に対してマイナス電圧が出力されるからです。　アンチログ回路は VBE の差に対して動作するので、Q2 のベース電位を上げるのと、Q1 のベース電位を下げるのとは同じ効果をもたらします。

アンチログ回路（電圧→電流変換回路）への入力は反転波形である必要があるのでU1の1倍反転増幅回路で波形を反転させています。$V_{in}$;正電圧→$I_{R2}$;負電流。

Analog 2.0風（共通エミッター）非反転版

U3周辺回路をQ2側につけ、Q1のコレクタ電流を出力とすると入力を反転させる必要がないようです。

Next Post Previous Post